Machine Learning Basics #
机器学习的定义与类型 #
定义 #
Machine Learning(机器学习) 是一种人工智能技术,核心目标是使计算机能够从数据中自动学习,并根据这些数据改进对特定任务的性能,而无需明确的编程指令。
机器学习通过以下三个要素实现:
- 数据(Data):输入的原始数据或特征数据。
- 模型(Model):表示学习的假设空间,决定如何从数据中学习模式。
- 优化目标(Object):定义如何评估模型好坏并改进其性能(如最小化误差)。
主要类型 #
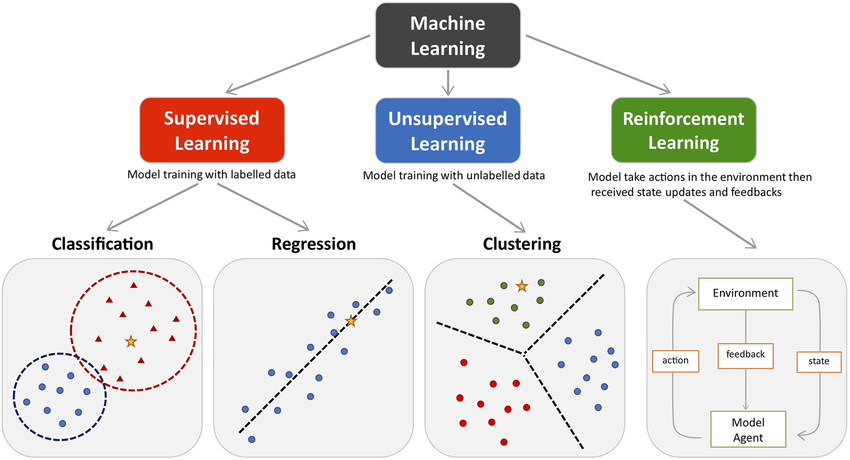
监督学习 (Supervised Learning) #
监督学习 (Supervised Learning) 从标记数据中学习。在这种情况下,输入数据及其对应的输出值被提供给算法,算法学习输入和输出值之间的映射(the mapping between the input and output values)。监督学习的目标是对新的、看不见的输入数据做出准确的预测。
输入(Input):特征数据 \(X\) 和目标变量 \(y\) (如标签或真实值)。
输出(Output):预测模型,用于对新数据进行分类或回归。
应用场景:
- 分类问题(Classification):将输入数据划分到预定义类别中。
- 回归问题(Regression):预测连续数值的目标变量。
无监督学习 (Unsupervised Learning) #
无监督学习 (Unsupervised Learning) 从未标记的数据中学习。在这种情况下,输入数据没有标记,算法自己学习在数据中寻找模式和结构。无监督学习的目标是发现数据中隐藏的模式和结构。
- 输入(Input):仅有特征数据 \(X\) 。
- 输出(Output):数据的潜在结构或表示。
- 应用场景:
- 聚类 (Clustering):将数据分组到不同簇中。
- 降维 (Dimensionality Reduction):简化数据表示,同时保留主要信息。
半监督学习 (Semi-Supervised Learning) #
半监督学习 (Semi-Supervised Learning) 从标记和未标记数据的组合中进行学习。在这种情况下,算法学习在未标记数据中寻找模式和结构,并使用标记数据来指导学习过程。
- 输入(Input):部分标注的数据和大量未标注的数据。
- 输出(Output):用于分类或回归的预测模型。
- 应用场景:
- 在标注数据有限或获取标签成本高昂的情况下(如医学影像标注)。
强化学习 (Reinforcement Learning) #
强化学习 (Reinforcement Learning) 通过与 环境(environment) 交互进行学习。在这种情况下,算法学习采取 行动(action) 来最大化环境提供的奖励信号。强化学习的目标是学习最大化长期 奖励(reward) 的 策略(policy)。
- 输入(Input):状态 \(S\) 、动作 \(A\) 、奖励 \(R\) 。
- 输出(Output):一个策略 \(\pi\) ,指引在不同状态下的最佳行动。
- 应用场景:
- 游戏 AI:如 AlphaGo 使用强化学习在围棋中击败人类选手。
- 机器人导航:训练机器人在环境中找到最佳路径。
显式(Explicit) 和 隐式(Implicit) #
在机器学习中,显式(Explicit) 和 隐式(Implicit) 通常用于描述模型、方法或表示的不同特性。它们反映了信息是直接表达出来还是通过间接方式体现。
显式(Explicit) 是指信息或结构是 直接表示 的,通常可以被明确地解释或观察到。
- 直接性:显式方法通常有清晰的数学公式或逻辑规则。
- 可解释性:显式模型的内部机制容易被理解。
- 可见性:输入到输出之间的关系是明确可见的。
- 示例:线性回归,逻辑回归,规则模型(决策树)。
隐式(Implicit) 是指信息或结构是通过 间接方式表示 的,不直接显现。
- 间接性:隐式方法通常不提供明确的公式,而是通过训练或优化过程间接捕获关系。
- 不可解释性:隐式模型的内部机制较难理解,通常被认为是“黑箱”。
- 抽象性:信息的表示可能分布在多个特征或参数中,而不是单一表达。
- 示例:神经网络,SVM,隐变量模型(Latent Variable Models)。
泛化能力(Generalization) #
机器学习的核心挑战在于,我们必须在新的、以前未见过的输入上表现良好——而不仅仅是我们的模型所训练的输入。在以前未观察到的输入上表现良好的能力称为泛化(generalization)。在训练过程中,我们通过降低 训练误差 (Training Error) 优化模型。但模型不仅需要在训练集上表现优异,还需要降低泛化误差 (Generalization Error),即 测试误差(Test Error)。
数据集(Datasets)分类和误差(Errors) #
训练集(Train Set) #
- 定义:训练集是模型学习的主要数据来源(占大多数),包括 输入特征 和对应的 目标输出(对于监督学习)。
- 功能:用于训练模型(的参数),通过优化算法最小化训练误差。
训练误差(Training Error):训练误差是模型在训练数据上的错误率。它是通过测量每个训练示例的预测输出(predicted output)与实际输出(actual output)之间的差异来计算的。由于模型是在此数据上训练的,因此预计它会在此数据上表现良好,并且训练误差通常较低。
验证集(Validation Set) #
- 定义:验证集是从训练数据中分离出来的一部分,用于评估模型在未见数据上的表现。
- 功能:
- 帮助调整超参数(如学习率、正则化系数、模型结构等)。
- 用于选择最佳模型,例如在多次训练后选择验证误差最低的模型。
验证误差(Validation Error):验证误差是模型在验证数据上的错误率。用于评估训练期间模型的性能,目标是找到验证误差最低的模型。
测试集(Test Set) #
- 定义:测试集是完全独立于训练和验证的数据,模型在训练和验证过程中从未接触过。
- 功能:用于评估模型的最终泛化性能,反映模型在实际场景中的表现。
测试误差(Test Error):测试误差是模型在测试数据上的错误率。测试数据是与训练和验证数据完全独立的数据集,用于评估模型的最终性能。测试误差是 最重要的误差指标,因为它告诉我们模型在新的、未见过的数据上的表现如何。
欠拟合 (Underfitting) #
- 定义:当模型过于简单而无法捕捉数据中的底层模式时,就会发生欠拟合。该模型具有高偏差和低方差,这意味着它在训练和测试数据上的表现都很差。
- 表现:
- 模型复杂度低,无法很好地拟合训练数据。
- 训练误差与测试误差都较大,模型性能较差。
- 原因:
- 模型过于简单,无法学习到数据中的复杂关系或特征。
- 特征不足,数据无法充分表达问题。
- 训练时间不足,模型未完全收敛。
- 解决方法:
- 增加模型复杂度:选择更复杂的模型(如从线性模型切换到非线性模型)。
- 增加特征:引入更多特征或通过特征工程提取更有效的特征。
- 延长训练时间:确保模型充分训练直到收敛。
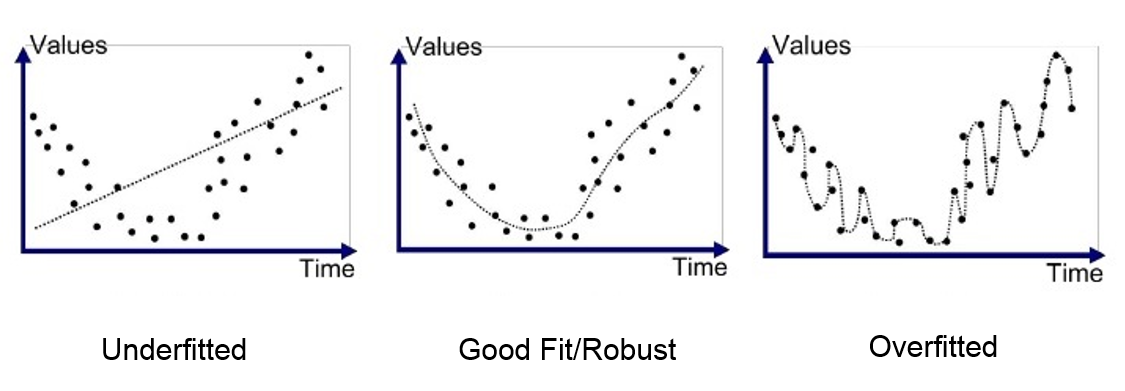
过拟合 (Overfitting) #
- 定义:当模型过于复杂,与训练数据的拟合度过高时,就会发生过度拟合,从而捕获数据中的噪声和随机波动。因此,该模型在新的、未见过的数据上表现不佳。
- 表现:
- 模型对训练数据拟合良好,训练误差很低。
- 测试误差较高,模型泛化能力差。
- 原因:
- 模型复杂度过高,学习到了训练数据中的噪声或无意义模式。
- 训练数据过少,噪声占比高。
- 缺乏正则化约束,模型自由度太高。
- 解决方法:
- 减少模型复杂度:降低模型自由度(如减少神经网络层数或节点数)。
- 增加数据量:收集更多样本,减少模型对噪声的敏感性。
- 正则化:
- \(L_1\) 正则化:鼓励稀疏性,减少不重要的参数。
- \(L_2\) 正则化:限制参数的幅度,防止过大权重。
- 交叉验证:通过交叉验证选择模型或超参数,避免过拟合。
偏差-方差权衡(Bias-Variance Tradeoff) #
偏差 (Bias) #
- 定义:偏差衡量模型预测值的期望值与真实值之间的偏离程度。
- 公式:
\[
\text{Bias} = E[f(x)] - f^*(x)
\]
- \(f(x)\) :模型的预测值
- \(f^*(x)\) :真实值或目标函数
方差 (Variance) #
- 定义:方差衡量模型在不同训练数据集上的预测值的变化幅度。
- 公式: \[ \text{Variance} = E[(f(x) - E[f(x)])^2] \]
- 方差的平方根称为标准差,表示为 \(SE(x)\)
总误差分解 #
模型的总误差(Expected Error)可以分解为三部分:偏差、方差和噪声。在实际应用中,我们需要平衡 Bias 和 Variance 以此来找到最小的 Expected Error,目标是找到偏差和方差的最佳平衡点,既能保证低训练误差,又能有良好的泛化能力。
\[ \text{Total Error} = \text{Bias}^2 + \text{Variance} + \text{Irreducible Noise} \]- \(\text{Bias}^2\) : 表示系统误差,与模型的表达能力有关。
- \(\text{Variance}\) : 表示模型对训练数据的敏感程度。
- \(\text{Irreducible Noise}\) : 数据中固有的随机噪声,无法通过任何模型降低。
Bias-Variance Tradeoff 理解 #
偏差-方差权衡指的是模型很好地拟合训练数据的能力(低偏差) 与其推广到新数据的能力(低方差) 之间的权衡。
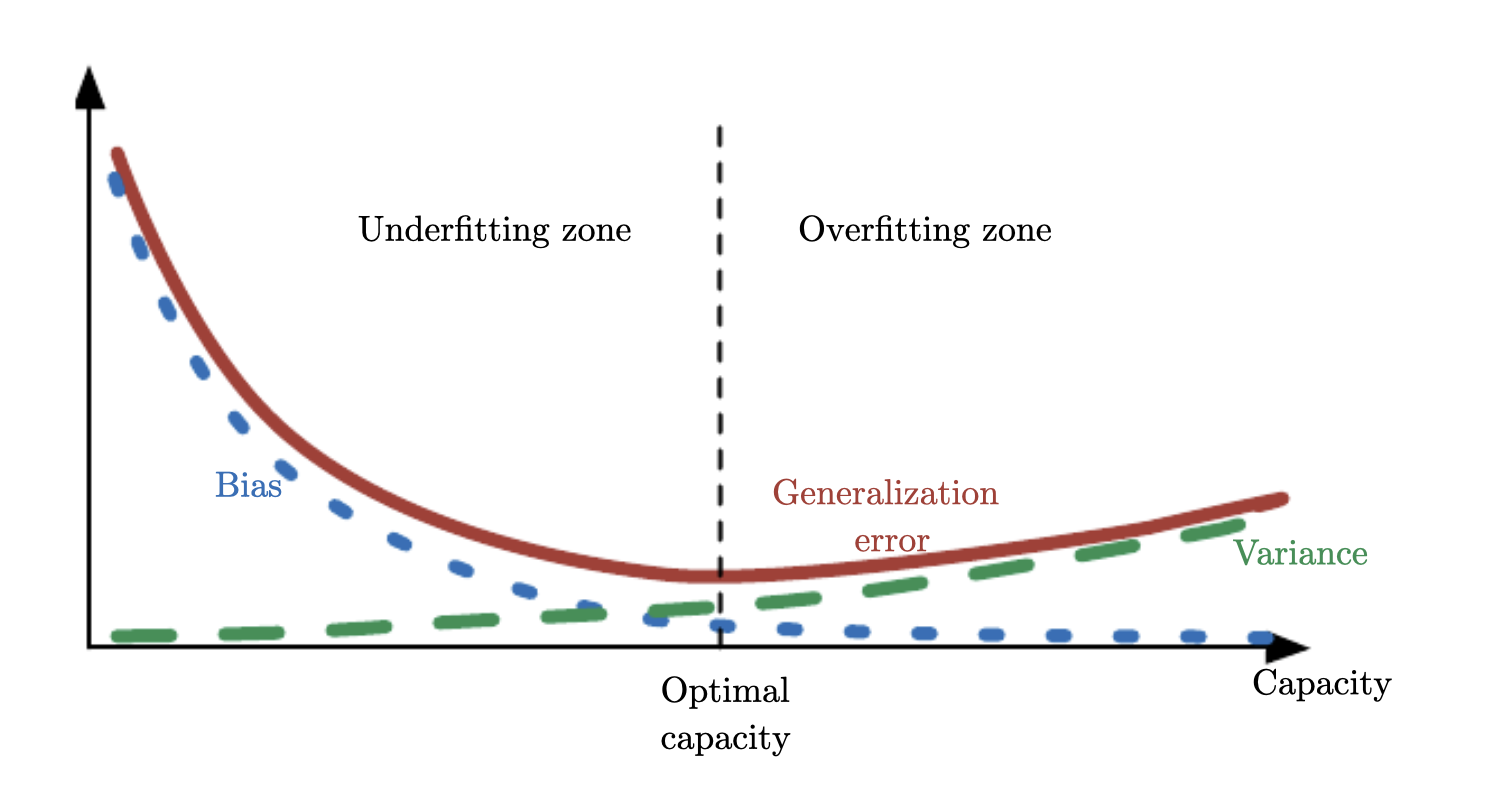
随着模型复杂度的增加,偏差趋于减小,方差趋于增大。如果模型太简单,它可能具有高偏差,这意味着它无法捕捉数据中的潜在模式,训练误差和测试误差会很高。如果模型太复杂,它可能具有高方差,这意味着它对训练数据中的噪声过于敏感,并且可能无法很好地推广到新数据,从而导致过度拟合。为了在偏差和方差之间取得平衡,我们需要找到模型的最佳复杂度。
- 低Bias但高Variance:复杂模型,过度拟合,表现为训练误差低但测试误差高。
- 高Bias但低Variance:简单模型,欠拟合,表现为训练误差和测试误差都高。
选择模型评估方法 #
- 交叉验证 (Cross-Validation):通过分割数据集来更好地估计模型的偏差和方差。
- 学习曲线 (Learning Curve):观察训练集误差和验证集误差随样本数量或模型复杂度变化的趋势,帮助分析模型的偏差和方差问题。
交叉验证(Cross Validation) #
交叉验证是机器学习中用于评估模型在独立数据集上性能的一种技术。交叉验证的基本思想是将可用数据分成两个或多个部分,其中一个部分用于训练模型,另一个部分用于验证模型。交叉验证用于通过提供模型对新数据的泛化程度的估计来防止过度拟合。它有效解决了仅用单一验证集或测试集可能导致的评估结果不稳定或偏差的问题。它也可以用于调整模型的超参数。
Note:在交叉验证(Cross-Validation)中,每一次计算的是 验证误差(validation error),而不是训练误差(training error)。交叉验证的目的是估计模型在未见数据上的性能,因此重点在于验证集的误差。
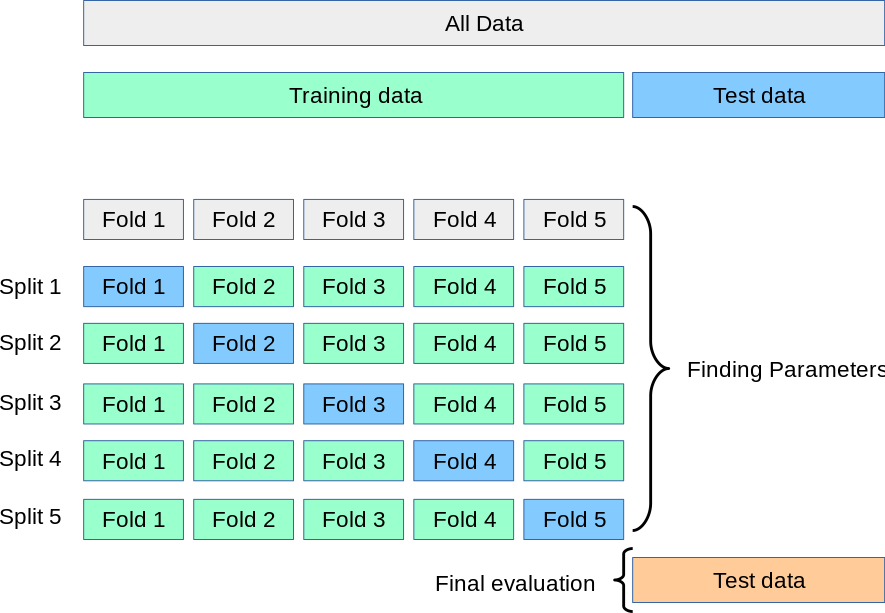
K折交叉验证 (K-Fold Cross-Validation) #
- 将数据集划分为 K 个不重叠的子集(folds)。每次取一个子集作为验证集,其余 K-1 个子集作为训练集。重复 K 次,每次更换验证集,最终对所有验证结果(Validation Error)取平均。
- 在
Cross-Validation的框架内,调节模型的hyperparameters,对使用不同参数的模型进行Cross-Validation验证。根据最终结果选择最佳模型。 - 在选择好最佳的
hyperparameters和模型后,用全部的数据进行训练。 - 使用完全独立的
Testset来评估模型的泛化能力。
优缺点: #
- 优点:可靠性高,适合数据量较大的情况。
- 缺点:当 K 较大时,计算成本较高。
K-Fold Cross-Validation 代码实现: #
# <--- From scratch --->
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# 简单的数据集生成
X = np.array([[i] for i in range(100)])
y = np.array([i*2 for i in range(100)])
model = LinearRegression()
def K_fold_CrossValidation(X, y, model, k=5):
# 数据集划分,按顺序划分为K个子集
fold = len(X) // k
error = []
for i in range(k):
val_start_idx = i * fold
val_end_idx = (i + 1) * fold
# 创建训练集和验证集
X_train = np.concatenate(X[:val_start_idx], X[val_end_idx:]),
y_train =np.concatenate(y[:val_start_idx], y[val_end_idx:])
X_val = X[val_start_idx:val_end_idx]
y_val = y[val_start_idx:val_end_idx]
# 使用模型进行训练和预测
model.fit(X_train, y_train)
y_pred = model.predict(X_val)
# 计算误差
curr_error = mean_squared_error(y_val, y_pred)
error.append(curr_error)
return np.mean(error)
# 执行交叉验证
avg_error = K_fold_CrossValidation(X, y, model, k=5)
print(f"Average cross-validation error: {avg_error}")
# <--- From scikit-learn --->
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
import numpy as np
# 生成数据集
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)
# 初始化模型
model = LinearRegression()
# 执行5折交叉验证,评分标准为负均方误差(neg_mean_squared_error)
scores = cross_val_score(
estimator=model, # estimator 类型对象,必须实现 fit 和 predict 方法。
X=X, # 特征数据
y=y, # 标签数据
cv=5, # 指定使用5折交叉验证
scoring='neg_mean_squared_error',
# 表示使用的评分方法(如 accuracy, neg_mean_squared_error, f1, roc_auc 等)
return_train_score=False # 不返回训练集得分,只返回验证集得分
)
# 输出每次折的误差
print(f"Cross-validation errors for each fold: {-scores}")
# 输出平均误差
print(f"Average cross-validation error: {-scores.mean()}")
留一法 (Leave-One-Out Cross-Validation, LOOCV) #
- 数据集中每个样本单独作为一次验证集,其余样本作为训练集。
- 模型训练次数等于样本数 N,最后计算所有验证集的误差平均值。
优缺点: #
- 优点:不浪费数据,最全面的评估方法。
- 缺点:计算代价极高,尤其是数据集较大时。
常见的机器学习完整流程 #
- 数据的准备和预处理
- 从数据库、API、文件等来源收集数据。
- 对所有的数据进行数据清洗 (e.g 处理缺失值,处理异常值,数据格式转换)
- 数据分割(训练集80%、验证集10%、测试集10%)
- 数据预处理 - 仅针对训练集(标准化/归一化,特征工程/选择/变换,Label Encoding,One-Hot Encoding)
- 模型训练与评估
- 选择模型:根据任务性质选择初始模型
- 设置交叉验证策略,交叉验证中的模型训练 - 使用训练集。
- 评估指标:不仅观察平均值(Validation Error),还需关注标准差,评估模型的稳定性。
- 超参数调优
- 网格搜索 (Grid Search):枚举所有可能的超参数组合,使用交叉验证评估每一组参数的表现。选择评估结果最优的参数组合。
- 随机搜索 (Random Search):从参数空间中随机采样一定数量的超参数组合进行评估。
- 测试集上的最终评估
- 固定最佳模型:在交叉验证确定的最佳超参数和模型结构上,重新训练模型,使用全体训练数据。
- 在测试集上评估:用测试集数据评估最终模型的性能,作为模型实际泛化能力的最终指标。Test Set 仅在最终测试时使用一次以防止数据泄漏(Data Leakage)