线性回归 #

线性回归（Linear Regression） #

线性回归是一种最简单的回归模型，目标是通过一个或多个输入变量预测一个 连续的（continuous） 输出变量。其核心思想是 拟合一条直线来描述输入（input）与输出（output）之间 的关系。其数学公式为：

\hat{y} = XW + b

其中 $N$ 是总样本数量， $\hat{y}$ 是预测值 $\in \mathbb{R}^{N \times 1}$ ， $X$ 是输入值 $\in \mathbb{R}^{N \times D}$ ， $W$ 是 Weight $\in \mathbb{R}^{D \times 1}$ ， $b$ 是 Bias $\in \mathbb{R}^{1}$ 。

损失函数（Loss Function） #

线性回归的训练目标是找到一组最优参数（权重 $W$ 和偏置 $b$ ），使得模型对训练数据的预测值与实际目标值之间的误差最小。具体来说，模型的目标是最小化误差函数（也称损失函数）。即使预测值 $\hat{y_{i}}$ 和实际值 $y_{i}$ 的差异最小化。

均方误差（Mean Squared Error, MSE） 是线性回归中最常用的损失函数。它计算预测值与真实值之间差异的平方和的均值：

MSE = \frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^2

通过调整参数 $W$ 和 $b$ ，最小化 $MSE$ 的目的是：

惩罚大的预测误差（使得较大的误差对总体损失影响更显著）。
保证损失函数是连续且可导的（continuously differentiable），方便优化算法（如梯度下降）进行求解。

梯度下降法在线性回归中的应用（Gradient Descent） #

在线性回归中，梯度下降通过调整模型参数 $W$ （权重）和 $b$ （偏置），逐步逼近最优解。我们通过对 Loss Funcion 求导（函数的切线）来实现这一点。切线（slope）的斜率就是该点的导数，它将为我们提供前进的方向。我们沿着下降最快的方向逐步降低 Loss Function。每一步的大小由参数 $\alpha$ 决定，该参数称为学习率。梯度下降算法可以表示为：

\begin{align*} &\frac{\partial L}{\partial w}= -\frac{2}{N}\sum_{i=1}^{N}(y_{i}-\hat{y_{i}})x_{i} \\ &\frac{\partial L}{\partial b}= -\frac{2}{N}\sum_{i=1}^{N}(y_{i}-\hat{y_{i}}) \\ & w := w - \alpha \frac{\partial L}{\partial w}, \quad b := b - \alpha \frac{\partial L}{\partial b} \\ \end{align*}

\begin{align*} &\mathrm{Repect\ until \ convergence} \{ \\ &\ \ \ \ w_{j}^{new} :=w_{j}^{old} - \alpha\frac{2}{N}\sum_{i=1}^{N}(y_{i}-\hat{y_{i}}) \ \ \ \ \mathrm{for} \ j = 0 \cdot\cdot\cdot d \\ &\} \\ \end{align*}

收敛准则
- 损失函数的变化小于某个阈值（如 $\Delta L < \epsilon$ ）。
- 达到预设的最大迭代次数。

学习率的影响 #

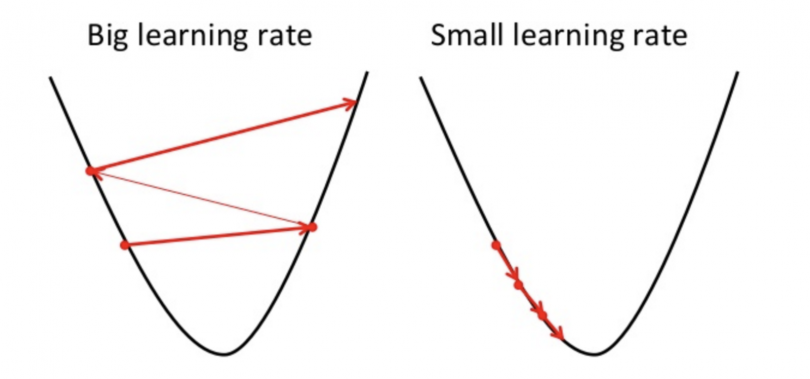
我们应该调整参数 $\alpha$ 以确保梯度下降算法在合理的时间内收敛。如果 $\alpha$ 太小，梯度下降可能会很慢。如果 $\alpha$ 太大，梯度下降可能会超过最小值。它可能无法收敛，甚至发散（ fail to converge, or even diverge）。无法收敛或花费太多时间获得最小值意味着我们的步长是错误的。

$\alpha$ 太大：可能导致更新过快，错过最优解，甚至发散。
$\alpha$ 太小：收敛速度慢，需要更多迭代。

性能评估（Evaluation Metrics） #

在训练完线性回归模型后，需要对模型的性能进行评估，以了解模型的拟合效果和预测能力。我们常使用均方根误差（RMSE）和确定系数（ $R^2$ 得分）来评估我们的模型。RMSE是残差平方和平均值的平方根。RMSE的定义是：

RMSE = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2}

$R^2$ 得分（ $R^2$ score）表示模型解释目标变量总变异的比例：。它可以被定义为：

R^2 = 1 - \frac{\sum_{i=1}^{N} (y_i - \hat{y}i)^2}{\sum_{i=1}^{N} (y_i - \bar{y})^2}

其中：

$\bar{y}$ 是目标值的均值。
$R^2$ 的取值范围是 [0, 1]（可以小于 0，表示模型比均值模型还差）。

解释：

$R^2 = 1$ ：模型能完全解释目标变量。
$R^2 = 0$ ：模型的表现与仅使用目标值均值的基准模型相同。
$R^2 < 0$ ：模型表现比基准模型差。

Linear Regression 代码实现 #

# <--- From scratch --->
import numpy as np
from sklearn.model_selection import train_test_split

# 生成数据：y = 2 + 3*X + 噪声
X = np.random.rand(100, 1)  # 随机生成100个样本，只有一个特征
y = 2 + 3 * X + np.random.rand(100, 1)  # 添加噪声项模拟真实数据

# 数据划分：80%训练集，20%测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 均方误差函数 (Mean Squared Error)
def MSE(y_1, y_2):
    return np.square(np.subtract(y_1, y_2)).mean()

# 均方根误差函数 (Root Mean Squared Error)
def RMSE(y_1, y_2):
    return np.sqrt(MSE(y_1, y_2))

# 线性回归的梯度下降实现
def LinearRegression_with_GD(X, y, learning_rate=0.001, threshold=0.001, max_iter=100):
    """
    X: 输入特征矩阵
    y: 输出目标向量
    learning_rate: 学习率，控制每次梯度更新的步长
    threshold: 损失函数收敛的阈值，差异小于该值则停止迭代
    max_iter: 最大迭代次数
    """
    # 添加偏置项 (Intercept term)
    X_new = np.concatenate((np.ones((X.shape[0], 1)), X), axis=1)  # 在特征矩阵前添加一列1
    total_sample, features = X_new.shape[0], X_new.shape[1]  # 获取样本数和特征数
    W = np.random.rand(features, 1)  # 初始化权重为随机值
    losses = []  # 用于记录每次迭代的损失值

    for i in range(max_iter):
        y_pred = np.dot(X_new, W)  # 计算预测值：h(X) = X_new * W
        loss = MSE(y_pred, y)  # 计算当前的MSE损失
        if losses and losses[-1] - loss < threshold:  # 如果损失下降小于阈值，提前停止
            losses.append(loss)
            break
        losses.append(loss)  # 记录当前损失
        gradient = np.dot(X_new.T, (np.subtract(y_pred, y)))  # 计算梯度：∇J(W)
        W -= learning_rate * gradient  # 使用梯度下降更新权重

    print("Final Training Loss:", losses[-1])  # 输出最终训练损失
    return W  # 返回训练好的权重

# 使用训练好的权重进行预测
def LinearRegression_Predict(X, y, W):
    """
    X: 输入特征矩阵
    y: 真实目标向量
    W: 已训练的权重
    """
    X_new = np.concatenate((np.ones((X.shape[0], 1)), X), axis=1)  # 添加偏置项
    y_pred = np.dot(X_new, W)  # 计算预测值：h(X) = X_new * W

    rmse = RMSE(y_pred, y)  # 计算均方根误差
    print("RMSE:", rmse)  # 输出预测的RMSE
    return y_pred  # 返回预测值

# 调用梯度下降实现线性回归
W = LinearRegression_with_GD(X_train, y_train)

# 使用训练好的模型预测测试集
y_pred = LinearRegression_Predict(X_test, y_test, W)

# <--- From scikit-learn --->
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import numpy as np

# 生成数据
X = np.random.rand(100, 1)  # 随机生成100个样本，每个样本只有一个特征
y = 2 + 3 * X + np.random.rand(100, 1)  # 模拟线性关系，并加入噪声

# 数据集分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建线性回归模型，设置可选参数
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)  # 用训练集拟合模型

# 预测测试集
y_pred = model.predict(X_test)  # 使用模型预测测试集

# 输出截距和权重
print("Intercept (Bias):", model.intercept_)  # 截距项
print("Coefficients (Weights):", model.coef_)  # 权重项

多项式回归（Polynomial Regression） #

多项式回归是一种线性回归的扩展形式，它适用于因变量与自变量之间呈现非线性关系的数据。通过在输入特征上应用多项式变换，进行了非线性扩展，将其映射到更高维的特征空间，使模型可以拟合复杂的非线性数据。多项式回归中，模型的参数（权重 $W$ ）仍然是线性求解的，因此它在数学本质上是线性模型。其数学公式为: $\hat{y} = X_{poly}W + b = W_{1}x + W_{2}x^2 + \cdots + W_{n}x^n + b$

特征处理：
- 线性回归：直接使用输入特征。
- 多项式回归：对输入特征进行非线性扩展。
拟合能力：
- 线性回归：只能拟合线性关系，容易欠拟合。
- 多项式回归：能够拟合非线性关系，但高次多项式可能导致过拟合。

多项式回归的步骤 #

数据准备：准备训练数据，其中包含输入特征（自变量）和目标值（因变量）。假设我们有一个简单的一维输入特征 $X$ 和目标值 $y$ ，目标是通过多项式回归来拟合这些数据。
特征工程：将原始特征扩展为多项式特征，使模型能够捕捉数据中的非线性关系。假设我们选择二次多项式（degree=2）。我们会将输入特征 $X = [1, 2, 3, 4, 5]$ 扩展为： $X_{\text{poly}} = \begin{bmatrix} 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \\ 1 & x_3 & x_3^2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & x_n^2 \end{bmatrix}$
模型训练：多项式回归本质上是在线性回归的基础上进行特征扩展。所以在特征扩展之后，我们依然使用线性回归的公式来训练模型： $\hat{y} = W_{0} + W_{1}x + W_{2}x^2 + \cdots + W_{n}x^n$ 回归模型的训练过程就是通过最小化 均方误差（MSE） 来求解模型的参数: $MSE = \frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2$
模型评估：通过训练误差和验证误差评估模型的性能。

Polynomial Regression 代码实现 #

# <--- From scikit-learn --->
import numpy as np
from sklearn.preprocessing import PolynomialFeatures  # 导入多项式特征扩展模块
from sklearn.linear_model import LinearRegression  # 导入线性回归模型
from sklearn.model_selection import train_test_split  # 导入数据集分割模块

# 生成随机数据作为输入
data = np.random.normal(size=(200, 2))  # 生成一个包含200个样本，2个特征的正态分布数据集
result = 2 + data[:, 0] ** 3 + 4 * data[:, 1]  # 计算目标值，包含多项式（3次方项和1次方项）
X_train, X_test, y_train, y_test = train_test_split(data, result, test_size=0.3, random_state=0)  # 将数据集划分为训练集和测试集，30%的数据为测试集

# 定义多项式回归函数
def Polynomial_Regression(train_input_features, train_outputs, prediction_features):
    # 创建多项式特征转换器，设置多项式的阶数为3（因为示例中包含3次方项）
    poly = PolynomialFeatures(degree=3)
    
    # 对训练数据进行拟合并转换，得到多项式特征
    X_poly_train = poly.fit_transform(train_input_features)

    # 训练线性回归模型
    model = LinearRegression()
    model.fit(X_poly_train, train_outputs)  # 用训练数据训练模型

    # 使用相同的多项式转换器对预测数据进行转换
    X_poly_pred = poly.transform(prediction_features)

    # 对转换后的数据进行预测
    predictions = model.predict(X_poly_pred)

    return predictions  # 返回预测结果

# 调用多项式回归函数进行预测
y_pred = Polynomial_Regression(X_train, y_train, X_test)